Hostname: page-component-6bf8c574d5-pdxrj Total loading time: 0 Render date: 2025-03-11T17:25:27.221Z Has data issue: false hasContentIssue false
  • English
  • Français

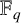ARITHMETIC-GEOMETRIC MEAN SEQUENCES OVER FINITE FIELDS $\mathbb {F}_q$, WHERE 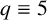$q\equiv 5$ (mod 8)

Part of: Miscellaneous applications of number theory General field theory

Published online by Cambridge University Press:  27 February 2025

NATÁLIA BÁTOROVÁ Open the ORCID record for NATÁLIA BÁTOROVÁ [Opens in a new window]  and
STEVAN GAJOVIĆ Open the ORCID record for STEVAN GAJOVIĆ [Opens in a new window]
NATÁLIA BÁTOROVÁ
Affiliation:
Faculty of Mathematics and Physics, Charles University, Sokolovská 83, 186 75 Praha 8, Czech Republic e-mail: [email protected]
STEVAN GAJOVIĆ*
Affiliation:
Faculty of Mathematics and Physics, Charles University, Sokolovská 83, 186 75 Praha 8, Czech Republic
*
e-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Arithmetic-geometric mean sequences were already studied over the real and complex numbers, and recently, Griffin et al. [‘AGM and jellyfish swarms of elliptic curves’, Amer. Math. Monthly 130(4) (2023), 355–369] considered them over finite fields 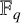$\mathbb {F}_q$ for 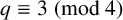$q \equiv 3 \pmod 4$. We extend the definition of arithmetic-geometric mean sequences over 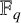$\mathbb {F}_q$ to 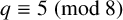$q \equiv 5 \pmod 8$. We explain the connection of these sequences with graphs and explore the properties of the graphs in the case where 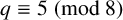$q \equiv 5 \pmod 8$.

Keywords

arithmetic-geometric mean sequencesfinite fieldsgraphs

MSC classification

Primary: 12E20: Finite fields (field-theoretic aspects)
Secondary: 11Z05: Miscellaneous applications of number theory
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , First View , pp. 1 - 12
Check for updates
Copyright
© The Author(s), 2025. Published by Cambridge University Press on behalf of Australian Mathematical Publishing Association Inc.

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

The second author was supported by the Czech Science Foundation GAČR, grant 21-00420M and a Junior Fund grant for postdoctoral positions at Charles University.

References

Bátorová, N., Arithmetic-Geometric Mean Sequences and Elliptic Curves Over Finite Fields. Bachelor thesis, Charles University, 2024.Google Scholar
Bondy, J. A. and Murty, U. S. R., Graph Theory with Applications (Elsevier Publishing Co., New York, 1976).CrossRefGoogle Scholar
Borwein, J. M. and Borwein, P. B., Pi and the AGM: A Study in Analytic Number Theory and Computational Complexity, Canadian Mathematical Society Series of Monographs and Advanced Texts, 8 (Wiley-Interscience, New York, 1987).Google Scholar
Carls, R., A Generalized Arithmetic Geometric Mean, PhD thesis, University of Groningen, 2024.Google Scholar
Cox, D., ‘The arithmetic-geometric mean of Gauss’, L’Enseignement Mathématique (2) 30(3-4) (1984), 275–330.Google Scholar
Cremona, J. E. and Thongjunthug, T., ‘The complex AGM, periods of elliptic curves over $\mathbb {C}$ and complex elliptic logarithms’, Journal of Number Theory 133(8) (2013), 2813–2841.CrossRefGoogle Scholar
Griffin, M. J., Ono, K., Saikia, N. and Tsai, W., ‘AGM and jellyfish swarms of elliptic curves’, Amer. Math. Monthly 130(4) (2023), 355–369.CrossRefGoogle Scholar
Kayath, J., Lane, C., Neifeld, B., Ni, T. and Xue, H., ‘AGM aquariums and elliptic curves over arbitrary finite fields’, Preprint, 2024, arXiv:2410.17969.Google Scholar
Small, C., ‘Sums of powers in large finite fields’, Proc. Amer. Math. Soc. 65(1) (1977), 35–36.CrossRefGoogle Scholar
Thongjunthug, T., Heights on Elliptic Curves over Number Fields, Period Lattices, and Complex Elliptic Logarithms, PhD thesis, University of Warwick, 2011.Google Scholar