Hostname: page-component-669899f699-7tmb6 Total loading time: 0 Render date: 2025-05-04T13:16:35.378Z Has data issue: false hasContentIssue false
  • English
  • Français

ALMOST ALL PRIMES HAVE A MULTIPLE OF SMALL HAMMING WEIGHT

Part of: Additive number theory; partitions Elementary number theory Sequences and sets Multiplicative number theory

Published online by Cambridge University Press:  23 May 2016

CHRISTIAN ELSHOLTZ
CHRISTIAN ELSHOLTZ*
Affiliation:
Institute of Analysis and Number Theory, Graz University of Technology, Kopernikusgasse 24, A-8010 Graz, Austria email [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We improve recent results of Bourgain and Shparlinski to show that, for almost all primes 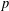$p$, there is a multiple 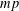$mp$ that can be written in binary as

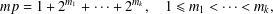$$\begin{eqnarray}mp=1+2^{m_{1}}+\cdots +2^{m_{k}},\quad 1\leq m_{1}<\cdots <m_{k},\end{eqnarray}$$
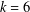with $k=6$ (corresponding to Hamming weight seven). We also prove that there are infinitely many primes 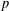$p$ with a multiplicative subgroup 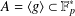$A=\langle g\rangle \subset \mathbb{F}_{p}^{\ast }$, for some 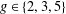$g\in \{2,3,5\}$, of size 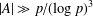$|A|\gg p/(\log p)^{3}$, where the sum–product set 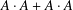$A\cdot A+A\cdot A$ does not cover 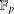$\mathbb{F}_{p}$ completely.

Keywords

primesadditive basessumsetsdistribution of integers with multiplicative constraintsWaring’s problem and variants

MSC classification

Primary: 11N25: Distribution of integers with specified multiplicative constraints
Secondary: 11A41: Primes 11A63: Radix representation; digital problems 11B13: Additive bases, including sumsets 11B50: Sequences (mod $m$) 11P05: Waring's problem and variants
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 94 , Issue 2 , October 2016 , pp. 224 - 235
Copyright
© 2016 Australian Mathematical Publishing Association Inc. 

References

Alon, N. and Bourgain, J., ‘Additive patterns in multiplicative subgroups’, Geom. Funct. Anal. 24(3) (2014), 721–739.Google Scholar
Baker, R. C. and Harman, G., ‘Shifted primes without large prime factors’, Acta Arith. 83(4) (1998), 331–361.Google Scholar
Ballot, C., ‘Density of prime divisors of linear recurrences’, Mem. Amer. Math. Soc. 115(551) (1995).Google Scholar
Bourgain, J., ‘New bounds on exponential sums related to the Diffie–Hellman distributions’, C. R. Math. Acad. Sci. Paris 338(11) (2004), 825–830.Google Scholar
Bourgain, J., ‘Mordell’s exponential sum estimate revisited’, J. Amer. Math. Soc. 18 (2005), 477–499.CrossRefGoogle Scholar
Bourgain, J., ‘Estimates on exponential sums related to the Diffie–Hellman distributions’, Geom. Funct. Anal. 15(1) (2005), 1–34.Google Scholar
Bourgain, J., Katz, N. and Tao, T., ‘A sum–product estimate in finite fields, and applications’, Geom. Funct. Anal. 14(1) (2004), 27–57.Google Scholar
Bundschuh, P., ‘Solution of problem 618’, Elem. Math. 26 (1971), 43–44.Google Scholar
Chapman, J., Erdoğan, M., Hart, D., Iosevich, A. and Koh, D., ‘Pinned distance sets, k-simplices, Wolff’s exponent in finite fields and sum–product estimates’, Math. Z. 271(1) (2012), 63–93.CrossRefGoogle Scholar
Cilleruelo, J. and Zumalacárregui, A., ‘An additive problem in finite fields of powers of elements of large multiplicative order’, Rev. Mat. Complut. 27(2) (2014), 501–508.CrossRefGoogle Scholar
Cochrane, T. and Pinner, C., ‘Sum-product estimates applied to Waring’s problem mod p ’, Integers 8 (2008), A46, 18 pp.Google Scholar
Cochrane, T., Hart, D., Pinner, C. and Spencer, C., ‘Waring’s number for large subgroups of ℤ p ∗ ’, Acta Arith. 163(4) (2014), 309–325.Google Scholar
Dietmann, R., Elsholtz, C. and Shparlinski, I., ‘On gaps between primitive roots in the Hamming metric’, Q. J. Math. 64(4) (2013), 1043–1055.Google Scholar
Elsholtz, C., ‘The distribution of sequences in residue classes’, Proc. Amer. Math. Soc. 130(8) (2002), 2247–2250.Google Scholar
Elsholtz, C., ‘The number 𝛤(k) in Waring’s problem’, Acta Arith. 131 (2008), 43–49.CrossRefGoogle Scholar
Erdős, P., ‘Bemerkungen zu einer Aufgabe in den Elementen’, Arch. Math. (Basel) 27(2) (1976), 159–163.CrossRefGoogle Scholar
Erdős, P. and Ram Murty, M., ‘On the order of a (mod p)’, in: Number Theory (Ottawa, 1996), CRM Proceedings and Lecture Notes, 19 (American Mathematical Society, Providence, RI, 1999), 87–97.Google Scholar
Ford, K., ‘The distribution of integers with a divisor in a given interval’, Ann. of Math. (2) 168 (2008), 367–433.Google Scholar
Garaev, M. Z. and Kueh, K. L., ‘Distribution of special sequences modulo a large prime’, Int. J. Math. Math. Sci. 50 (2003), 3189–3194.Google Scholar
Glibichuk, A. A., ‘Additive properties of product sets in an arbitrary finite field’, Preprint, arXiv:0801.2021, 2008.Google Scholar
Glibichuk, A. A., ‘Sums of powers of subsets of an arbitrary finite field’, Izv. Ross. Akad. Nauk Ser. Mat. 75(20) (2011), 35–68 (in Russian); translation in Izv. Math. 75(2) (2011), 253–285.Google Scholar
Glibichuk, A. A. and Rudnev, M., ‘On additive properties of product sets in an arbitrary finite field’, J. Anal. Math. 108 (2009), 159–170.Google Scholar
Harman, G., ‘On the greatest prime factor of p - 1 with effective constants’, Math. Comp. 74(252) (2005), 2035–2041.Google Scholar
Hart, D., ‘A note on sumsets of subgroups in ℤ p ∗ ’, Acta Arith. 161 (2013), 387–395.Google Scholar
Hart, D. and Iosevich, A., ‘Sums and products in finite fields: an integral geometric viewpoint’, in: Contemporary Mathematics, 464 (American Mathematical Society, Providence, RI, 2008), 129–135.Google Scholar
Hasse, H., ‘Über die Dichte der Primzahlen p, für die eine vorgegebene ganzrationale Zahl a≠0 von gerader bzw. ungerader Ordnung mod p ist’, Math. Ann. 166 (1966), 19–23.CrossRefGoogle Scholar
Heath-Brown, D. R., ‘Artin’s conjecture for primitive roots’, Q. J. Math. Oxford Ser. 2 37(1) (1986), 27–38.Google Scholar
Heath-Brown, D. R. and Konyagin, S., ‘New bounds for Gauss sums derived from kth powers and for Heilbronn’s exponential sum’, Q. J. Math. 51(2) (2000), 221–235.CrossRefGoogle Scholar
Hooley, C., ‘On Artin’s conjecture’, J. reine angew. Math. 225 (1967), 209–220.Google Scholar
Indlekofer, K.-H. and Timofeev, N. M., ‘Divisors of shifted primes’, Publ. Math. Debrecen 60 (2002), 307–345.Google Scholar
Kurlberg, P. and Pomerance, C., ‘On the periods of the linear congruential and power generators’, Acta Arith. 119(2) (2005), 149–169.Google Scholar
Luca, F. and Stanica, P., ‘Prime divisors of Lucas sequences and a conjecture of Skałba’, Int. J. Number Theory 1(1) (2005), 583–591.Google Scholar
Matthews, C. R., ‘Counting points modulo p for some finitely generated subgroups of algebraic groups’, Bull. Lond. Math. Soc. 14 (1982), 149–154.Google Scholar
Moree, P., ‘On the divisors of a k + b k ’, Acta Arith. 80(3) (1997), 197–212.Google Scholar
Moree, P., ‘Artin’s primitive root conjecture—a survey’, Integers 12A A13 (2012).Google Scholar
Odoni, R. W. K., ‘A conjecture of Krishnamurthy on decimal periods and some allied problems’, J. Number Theory 13(3) (1981), 303–319.Google Scholar
Pappalardi, F., ‘On the order of finitely generated subgroups of Q ∗ (mod p) and divisors of p - 1’, J. Number Theory 57(2) (1996), 207–222.Google Scholar
Rudnev, M., ‘An improved estimate on sums of product sets’, arXiv:0805.2696v1, 2008.Google Scholar
Schoen, T. and Shkredov, I. D., ‘Additive properties of multiplicative subgroups of F p ’, Q. J. Math. 63(3) (2012), 713–722.Google Scholar
Shkredov, I. D., ‘Some new inequalities in additive combinatorics’, Mosc. J. Comb. Number Theory 3(3–4) (2013), 189–239.Google Scholar
Shkredov, I. D., ‘On exponential sums over multiplicative subgroups of medium size’, Finite Fields Appl. 30 (2014), 72–87.Google Scholar
Shparlinski, I. E., ‘Prime divisors of sparse integers’, Period. Math. Hungar. 46(2) (2003), 215–222.Google Scholar
Shparlinski, I. E., ‘Exponential sums and prime divisors of sparse integers’, Period. Math. Hungar. 57(1) (2008), 93–99.Google Scholar
Skałba, M., ‘Two conjectures on primes dividing 2 a + 2 b + 1’, Elem. Math. 59(4) (2004), 171–173.CrossRefGoogle Scholar
Stolarsky, K. B., ‘Integers whose multiples have anomalous digital frequencies’, Acta Arith. 38 (1980), 117–128.Google Scholar
Tao, T., ‘A remark on primality testing and decimal expansions’, J. Aust. Math. Soc. 91(3) (2011), 405–413.Google Scholar
Wagstaff, S. Jr., ‘Prime numbers with a fixed number of one bits or zero bits in their binary representation’, Experiment. Math. 10(2) (2001), 267–274.Google Scholar
Weil, A., ‘Numbers of solutions of equations in finite fields’, Bull. Amer. Math. Soc. 55 (1949), 497–508.Google Scholar
Wiertelak, K., ‘On the density of some sets of primes. IV’, Acta Arith. 43(2) (1984), 177–190.Google Scholar