No CrossRef data available.
Published online by Cambridge University Press: 15 November 2023
Two sets 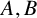 $A,B$ of positive integers are called exact additive complements if
$A,B$ of positive integers are called exact additive complements if 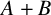 $A+B$ contains all sufficiently large integers and
$A+B$ contains all sufficiently large integers and 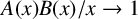 $A(x)B(x)/x\rightarrow 1$. For
$A(x)B(x)/x\rightarrow 1$. For 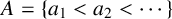 $A=\{a_1<a_2<\cdots \}$, let
$A=\{a_1<a_2<\cdots \}$, let 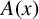 $A(x)$ denote the counting function of A and let
$A(x)$ denote the counting function of A and let 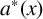 $a^*(x)$ denote the largest element in
$a^*(x)$ denote the largest element in 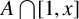 $A\bigcap [1,x]$. Following the work of Ruzsa [‘Exact additive complements’, Quart. J. Math. 68 (2017) 227–235] and Chen and Fang [‘Additive complements with Narkiewicz’s condition’, Combinatorica 39 (2019), 813–823], we prove that, for exact additive complements
$A\bigcap [1,x]$. Following the work of Ruzsa [‘Exact additive complements’, Quart. J. Math. 68 (2017) 227–235] and Chen and Fang [‘Additive complements with Narkiewicz’s condition’, Combinatorica 39 (2019), 813–823], we prove that, for exact additive complements 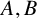 $A,B$ with
$A,B$ with 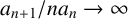 ${a_{n+1}}/ {na_n}\rightarrow \infty $,
${a_{n+1}}/ {na_n}\rightarrow \infty $, 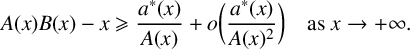 $$ \begin{align*}A(x)B(x)-x\geqslant \frac{a^*(x)}{A(x)}+o\bigg(\frac{a^*(x)}{A(x)^2}\bigg) \quad\mbox{as } x\rightarrow +\infty.\end{align*} $$
$$ \begin{align*}A(x)B(x)-x\geqslant \frac{a^*(x)}{A(x)}+o\bigg(\frac{a^*(x)}{A(x)^2}\bigg) \quad\mbox{as } x\rightarrow +\infty.\end{align*} $$
We also construct exact additive complements 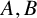 $A,B$ with
$A,B$ with 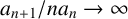 ${a_{n+1}}/{na_n}\rightarrow \infty $ such that
${a_{n+1}}/{na_n}\rightarrow \infty $ such that 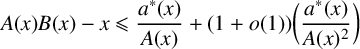 $$ \begin{align*}A(x)B(x)-x\leqslant \frac{a^*(x)}{A(x)}+(1+o(1))\bigg(\frac{a^*(x)}{A(x)^2}\bigg)\end{align*} $$
$$ \begin{align*}A(x)B(x)-x\leqslant \frac{a^*(x)}{A(x)}+(1+o(1))\bigg(\frac{a^*(x)}{A(x)^2}\bigg)\end{align*} $$
for infinitely many positive integers x.
The first author is supported by the National Natural Science Foundation of China, Grant No. 12171246 and the Natural Science Foundation of Jiangsu Province, Grant No. BK20211282. The second author is supported by the NKFIH Grant No. K129335 and the National Research, Development and Innovation Fund Grant No. KKP144059 ‘Fractal geometry and applications’.