Hostname: page-component-669899f699-tzmfd Total loading time: 0 Render date: 2025-05-06T04:46:24.574Z Has data issue: false hasContentIssue false
  • English
  • Français

ON THE SET OF KRONECKER NUMBERS

Part of: Multiplicative number theory

Published online by Cambridge University Press:  08 March 2024

SAYAN GOSWAMI ,
WEN HUANG  and
XIAOSHENG WU
SAYAN GOSWAMI*
Affiliation:
The Institute of Mathematical Sciences, A CI of Homi Bhabha National Institute, CIT Campus, Taramani, Chennai 600113, India
WEN HUANG
Affiliation:
School of Mathematical Sciences, University of Science and Technology of China, Hefei 230026, PR China e-mail: [email protected]
XIAOSHENG WU
Affiliation:
School of Mathematics, Hefei University of Technology, Hefei 230009, PR China e-mail: [email protected]
*
e-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

A positive even number is said to be a Maillet number if it can be written as the difference between two primes, and a Kronecker number if it can be written in infinitely many ways as the difference between two primes. It is believed that all even numbers are Kronecker numbers. We study the division and multiplication of Kronecker numbers and show that these numbers are rather abundant. We prove that there is a computable constant k and a set D consisting of at most 720 computable Maillet numbers such that, for any integer n, 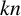$kn$ can be expressed as a product of a Kronecker number and a Maillet number in D. We also prove that every positive rational number can be written as a ratio of two Kronecker numbers.

Keywords

difference of primesKronecker numberΔr*-setIP-set

MSC classification

Primary: 11N05: Distribution of primes
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 110 , Issue 2 , October 2024 , pp. 262 - 270
Check for updates
Copyright
© The Author(s), 2024. Published by Cambridge University Press on behalf of Australian Mathematical Publishing Association Inc.

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

Footnotes

The second author was supported in part by NSFC (Grant Nos. 12090012, 12090010) and the third author was supported in part by NSFC (Grant No. 12271135).

References

Fish, A., ‘On product of difference sets for sets of positive density’, Proc. Amer. Math. Soc. 146(8) (2018), 3449–3453.10.1090/proc/14078CrossRefGoogle Scholar
Goldston, D. A., Pintz, J. and Yildirim, C. Y., ‘Primes in tuples. I’, Ann. of Math. (2) 170(2) (2009), 819–862.10.4007/annals.2009.170.819CrossRefGoogle Scholar
Goswami, S., ‘Product of difference sets of set of primes’, Proc. Amer. Math. Soc. 151(12) (2023), 5081–5086.Google Scholar
Granville, A., Kane, D. M., Koukoulopoulos, D. and Lemke Oliver, R. J., ‘Best possible densities of Dickson $m$ -tuples, as a consequence of Zhang–Maynard–Tao’, in: Analytic Number Theory (eds. Pomerance, C. and Rassias, M. T.) (Springer, Cham, 2015), 133–144.10.1007/978-3-319-22240-0_10CrossRefGoogle Scholar
Green, B. and Tao, T., ‘Linear equations in primes’, Ann. of Math. (2) 171(3) (2010), 1753–1850.10.4007/annals.2010.171.1753CrossRefGoogle Scholar
Green, B. and Tao, T., ‘The Möbius function is strongly orthogonal to nilsequences’, Ann. of Math. (2) 175(2) (2012), 541–566.10.4007/annals.2012.175.2.3CrossRefGoogle Scholar
Green, B., Tao, T. and Ziegler, T., ‘An inverse theorem for the Gowers ${U}^{s+1}[N]$ -norm’, Ann. of Math. (2) 176(3) (2012), 1231–1372.10.4007/annals.2012.176.2.11CrossRefGoogle Scholar
Hindman, N., ‘Finite sums from sequenceses within cells of partitions of $\mathbb{N}$ ’, J. Combin. Theory Ser. A 17 (1974), 1–11.10.1016/0097-3165(74)90023-5CrossRefGoogle Scholar
Hindman, N. and Strauss, D., Algebra in the Stone–Čech Compactification: Theory and Applications, 2nd edn (de Gruyter, Berlin, 2012).Google Scholar
Huang, W. and Wu, X., ‘On the set of the difference of primes’, Proc. Amer. Math. Soc. 145(9) (2017), 3787–3793.10.1090/proc/13533CrossRefGoogle Scholar
Kronecker, L., Vorlesungen über Zahlentheorie, I (Teubner, Leipzig, 1901), 68.Google Scholar
Maynard, J., ‘Small gaps between primes’, Ann. of Math. (2) 181(1) (2015), 383–414.10.4007/annals.2015.181.1.7CrossRefGoogle Scholar
Pintz, J., ‘Polignac numbers, conjectures of Erdős on gaps between primes, arithmetic progressions in primes, and the bounded gap conjecture’, in: From Arithmetic to Zeta-Functions (eds. Sander, J., Steuding, J. and Steuding, R.) (Springer, Cham, 2016), 367–384.Google Scholar
Polymath, D. H. J., ‘Variants of the Selberg sieve, and bounded intervals containing many primes’, Res. Math. Sci. 1 (2014), Article no. 12.10.1186/s40687-014-0012-7CrossRefGoogle Scholar
Zhang, Y., ‘Bounded gaps between primes’, Ann. of Math. (2) 179(3) (2014), 1121–1174.10.4007/annals.2014.179.3.7CrossRefGoogle Scholar