No CrossRef data available.
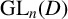 $\mathrm {GL}_n(D)$
$\mathrm {GL}_n(D)$Published online by Cambridge University Press: 06 November 2024
Let A be an F-central simple algebra of degree 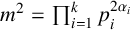 $m^2=\prod _{i=1}^k p_i^{2\alpha _i}$ and G be a subgroup of the unit group of A such that
$m^2=\prod _{i=1}^k p_i^{2\alpha _i}$ and G be a subgroup of the unit group of A such that 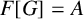 $F[G]=A$. We prove that if G is a central product of two of its subgroups M and N, then
$F[G]=A$. We prove that if G is a central product of two of its subgroups M and N, then 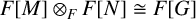 $F[M]\otimes _F F[N]\cong F[G]$. Also, if G is locally nilpotent, then G is a central product of subgroups
$F[M]\otimes _F F[N]\cong F[G]$. Also, if G is locally nilpotent, then G is a central product of subgroups 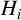 $H_i$, where
$H_i$, where 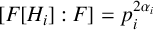 $[F[H_i]:F]=p_i^{2\alpha _i}$,
$[F[H_i]:F]=p_i^{2\alpha _i}$, 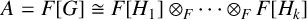 $A=F[G]\cong F[H_1]\otimes _F \cdots \otimes _F F[H_k]$ and
$A=F[G]\cong F[H_1]\otimes _F \cdots \otimes _F F[H_k]$ and 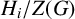 $H_i/Z(G)$ is the Sylow
$H_i/Z(G)$ is the Sylow 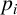 $p_i$-subgroup of
$p_i$-subgroup of 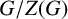 $G/Z(G)$ for each i with
$G/Z(G)$ for each i with 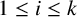 $1\leq i\leq k$. Additionally, there is an element of order
$1\leq i\leq k$. Additionally, there is an element of order 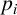 $p_i$ in F for each i with
$p_i$ in F for each i with 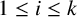 $1\leq i\leq k$.
$1\leq i\leq k$.