Hostname: page-component-669899f699-8p65j Total loading time: 0 Render date: 2025-04-30T20:47:25.214Z Has data issue: false hasContentIssue false
  • English
  • Français

THE GROWTH OF SOLUTIONS OF MONGE–AMPÈRE EQUATIONS IN HALF SPACES AND ITS APPLICATION

Part of: Partial differential equations Elliptic equations and systems

Published online by Cambridge University Press:  31 March 2023

SHANSHAN MA Open the ORCID record for SHANSHAN MA [Opens in a new window]  and
XIAOBIAO JIA Open the ORCID record for XIAOBIAO JIA [Opens in a new window]
SHANSHAN MA
Affiliation:
School of Mathematics and Statistics, Zhengzhou University, Zhengzhou 450001, PR China e-mail: [email protected]
XIAOBIAO JIA*
Affiliation:
School of Mathematics and Statistics, North China University of Water Resources and Electric Power, Zhengzhou 450046, PR China
*
e-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We consider the growth of the convex viscosity solution of the Monge–Ampère equation 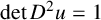$\det D^2u=1$ outside a bounded domain of the upper half space. We show that if u is a convex quadratic polynomial on the boundary 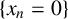$\{x_n=0\}$ and there exists some 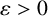$\varepsilon>0$ such that 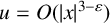$u=O(|x|^{3-\varepsilon })$ at infinity, then 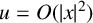$u=O(|x|^2)$ at infinity. As an application, we improve the asymptotic result at infinity for viscosity solutions of Monge–Ampère equations in half spaces of Jia, Li and Li [‘Asymptotic behavior at infinity of solutions of Monge–Ampère equations in half spaces’, J. Differential Equations 269(1) (2020), 326–348].

Keywords

Monge–Ampère equationgrowthasymptotic behaviour

MSC classification

Primary: 35J96: Elliptic Monge-Ampère equations
Secondary: 35B40: Asymptotic behavior of solutions
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 109 , Issue 1 , February 2024 , pp. 125 - 137
Check for updates
Copyright
© The Author(s), 2023. Published by Cambridge University Press on behalf of Australian Mathematical Publishing Association Inc.

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

Footnotes

The first author was supported by Natural Science Foundation of Henan Province (Grant No. 222300420321); the second author was supported by Natural Science Foundation of Henan Province (Grant No. 222300420232).

References

Caffarelli, L. A. and Li, Y. Y., ‘An extension to a theorem of Jörgens, Calabi and Pogorelov’, Comm. Pure Appl. Math. 56(5) (2003), 549–583.CrossRefGoogle Scholar
Figalli, A., The Monge–Ampère Equation and Its Applications, Zurich Lectures in Advanced Mathematics (European Mathematical Society (EMS), Zürich, 2017).CrossRefGoogle Scholar
Gilbarg, D. and Trudinger, N. S., Elliptic Partial Differential Equations of Second Order, Classics in Mathematics, 224 (Springer-Verlag, Berlin, 2001).CrossRefGoogle Scholar
Gutiérrez, C. E., The Monge–Ampère Equation, 2nd edn, Progress in Nonlinear Differential Equations and their Applications, 89 (Birkhäuser/Springer, Cham, 2016).CrossRefGoogle Scholar
Jia, X. B., Li, D. S. and Li, Z. S., ‘Asymptotic behavior at infinity of solutions of Monge–Ampère equations in half spaces’, J. Differential Equations 269(1) (2020), 326–348.CrossRefGoogle Scholar
Mooney, C., ‘Partial regularity for singular solutions to the Monge–Ampère equation’, Comm. Pure Appl. Math. 68(6) (2015), 1066–1084.CrossRefGoogle Scholar
Mooney, C., The Monge–Ampère equation, available online at https://www.math.uci.edu/~mooneycr/MongeAmpere_Notes.pdf.Google Scholar
Savin, O., ‘Pointwise ${C}^{2,\alpha }$ estimates at the boundary for the Monge–Ampère equation’, J. Amer. Math. Soc. 26(1) (2013), 63–99.CrossRefGoogle Scholar
Savin, O., ‘A localization theorem and boundary regularity for a class of degenerate Monge–Ampère equations’, J. Differential Equations 256(2) (2014), 327–388.CrossRefGoogle Scholar
Yan, M., ‘Extension of convex function’, J. Convex Anal. 21(4) (2014), 965–987.Google Scholar
Zhou, Z. W., Gong, S. Y. and Bao, J. G., ‘Ancient solutions of exterior problem of parabolic Monge–Ampère equations’, Ann. Mat. Pura Appl. (4) 200(4) (2021), 1605–1624.CrossRefGoogle Scholar