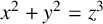Hostname: page-component-669899f699-qzcqf Total loading time: 0 Render date: 2025-05-01T10:46:23.176Z Has data issue: false hasContentIssue false
  • English
  • Français

FROBENIUS NUMBERS ASSOCIATED WITH DIOPHANTINE TRIPLES OF $x^2+y^2=z^3$

Part of: Semigroups Diophantine equations Combinatorics

Published online by Cambridge University Press:  14 November 2024

TAKAO KOMATSU Open the ORCID record for TAKAO KOMATSU [Opens in a new window] ,
NEHA GUPTA Open the ORCID record for NEHA GUPTA [Opens in a new window]  and
MANOJ UPRETI Open the ORCID record for MANOJ UPRETI [Opens in a new window]
TAKAO KOMATSU*
Affiliation:
Faculty of Education, Nagasaki University, Nagasaki 852-8521, Japan
NEHA GUPTA
Affiliation:
Department of Mathematics, School of Natural Sciences, Shiv Nadar Institute of Eminence, Gautam Buddha Nagar, Greater Noida 201314, India e-mail: [email protected]
MANOJ UPRETI
Affiliation:
Department of Mathematics, School of Natural Sciences, Shiv Nadar Institute of Eminence, Gautam Buddha Nagar, Greater Noida 201314, India e-mail: [email protected]
*
e-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We give an explicit formula for the Frobenius number of triples associated with the Diophantine equation 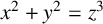$x^2+y^2=z^3$, that is, the largest positive integer that can only be represented in p ways by combining the three integers of the solutions of 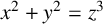$x^2+y^2=z^3$. For the equation 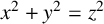$x^2+y^2=z^2$, the Frobenius number has already been given. Our approach can be extended to the general equation 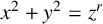$x^2+y^2=z^r$ for 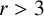$r>3$.

Keywords

Frobenius problemDiophantine equationPythagorean tripleApéry set

MSC classification

Primary: 11D07: The Frobenius problem
Secondary: 05A15: Exact enumeration problems, generating functions 11D04: Linear equations 11D25: Cubic and quartic equations 20M14: Commutative semigroups
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , First View , pp. 1 - 10
Check for updates
Copyright
© The Author(s), 2024. Published by Cambridge University Press on behalf of Australian Mathematical Publishing Association Inc.

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

Footnotes

The first author was supported by JSPS KAKENHI Grant Number 24K22835.

References

Brauer, A. and Shockley, B. M., ‘On a problem of Frobenius’, J. reine angew. Math. 211 (1962), 215–220.Google Scholar
Chaichana, T., Komatsu, T. and Laohakosol, V., ‘On convergents of certain values of hyperbolic functions formed from Diophantine equations’, Tokyo J. Math. 36(1) (2013), 239–251.CrossRefGoogle Scholar
Curtis, F., ‘On formulas for the Frobenius number of a numerical semigroup’, Math. Scand. 67 (1990), 190–192.CrossRefGoogle Scholar
Elsner, C., Komatsu, T. and Shiokawa, I., ‘On convergents formed by Pythagorean numbers’, in: Diophantine Analysis and Related Fields 2006. In honor of Iekata Shiokawa. Proceedings of the Conference, Keio University, Yokohama, Japan, March 7–10, 2006, Department of Mathematics, Seminar on Mathematical Sciences, 35 (eds. Katsurada, M., Komatsu, T. and Nakada, H.) (Keio University, Yokohama, 2006), 59–76.Google Scholar
Elsner, C., Komatsu, T. and Shiokawa, I., ‘Approximation of values of hypergeometric functions by restricted rationals’, J. Théor. Nombres Bordeaux 19(2) (2007), 393–404.CrossRefGoogle Scholar
Elsner, C., Komatsu, T. and Shiokawa, I., ‘On convergents formed from Diophantine equations’, Glas. Mat. Ser. III 44(2) (2009), 267–284.CrossRefGoogle Scholar
Gil, B. K., Han, J.-W., Kim, T. H., Koo, R. H., Lee, B. W., Lee, J., Nam, K. S., Park, H. W. and Park, P.-S., ‘Frobenius numbers of Pythagorean triples’, Int. J. Number Theory 11(2) (2015), 613–619.CrossRefGoogle Scholar
Komatsu, T., ‘The Frobenius number for sequences of triangular numbers associated with number of solutions’, Ann. Comb. 26 (2022), 757–779.CrossRefGoogle Scholar
Komatsu, T., ‘The Frobenius number associated with the number of representations for sequences of repunits’, C. R. Math. Acad. Sci. Paris 361 (2023), 73–89.CrossRefGoogle Scholar
Komatsu, T., ‘On the determination of $p$ -Frobenius and related numbers using the $p$ -Apéry set’, Rev. R. Acad. Cienc. Exactas Fís. Nat. Ser. A Mat. RACSAM 118 (2024), Article no. 58, 17 pages.Google Scholar
Komatsu, T., Gupta, N. and Upreti, M., ‘Frobenius numbers associated with Diophantine triples of ${x}^2+{y}^2={z}^r$ ’ (extended version), Preprint, 2024, arXiv:2403.07534.Google Scholar
Komatsu, T., Laishram, S. and Punyani, P., ‘ $p$ -numerical semigroups of generalized Fibonacci triples’, Symmetry 15(4) (2023), Article no. 852, 13 pages.CrossRefGoogle Scholar
Komatsu, T. and Pita-Ruiz, C., ‘The Frobenius number for Jacobsthal triples associated with number of solutions’, Axioms 12(2) (2023), Article no. 98, 18 pages.CrossRefGoogle Scholar
Komatsu, T. and Ying, H., ‘The $p$ -Frobenius and $p$ -Sylvester numbers for Fibonacci and Lucas triplets’, Math. Biosci. Eng. 20(2) (2023), 3455–3481.CrossRefGoogle Scholar
Komatsu, T. and Ying, H., ‘The $p$ -numerical semigroup of the triple of arithmetic progressions’, Symmetry 15(7) (2023), Article no. 1328, 17 pages.CrossRefGoogle Scholar
Komatsu, T. and Ying, H., ‘ $p$ -numerical semigroups with $p$ -symmetric properties’, J. Algebra Appl. 23(13) (2024), Article no. 2450216.Google Scholar
Liu, F. and Xin, G., ‘A fast algorithm for denumerants with three variables’, Preprint, 2024, arXiv:2406.18955.CrossRefGoogle Scholar
Liu, F., Xin, G. and Zhang, C., ‘Three simple reduction formulas for the denumerant functions’, Ramanujan J. 65 (2024), 1567–1577.CrossRefGoogle Scholar
Rosales, J. C., Branco, M. B. and Torrão, D., ‘The Frobenius problem for Mersenne numerical semigroups’, Math. Z. 286 (2017), 741–749.CrossRefGoogle Scholar
Selmer, E. S., ‘On the linear diophantine problem of Frobenius’, J. reine angew. Math. 293/294 (1977), 1–17.Google Scholar
Sylvester, J. J., ‘On subinvariants, i.e. semi-invariants to binary quantics of an unlimited order’, Amer. J. Math. 5 (1882), 119–136.CrossRefGoogle Scholar
Sylvester, J. J., ‘Mathematical questions with their solutions’, Educational Times 41 (1884), 21.Google Scholar
Yin, R. and Komatsu, T., ‘Frobenius numbers associated with Diophantine triples of ${x}^2-{y}^2={z}^r$ ’, Symmetry 16(7) (2024), Article no. 855, 16 pages.CrossRefGoogle Scholar