Hostname: page-component-669899f699-chc8l Total loading time: 0 Render date: 2025-04-30T19:50:43.354Z Has data issue: false hasContentIssue false
  • English
  • Français

2-LOCAL ISOMETRIES OF SOME NEST ALGEBRAS

Part of: Special classes of linear operators Linear spaces and algebras of operators

Published online by Cambridge University Press:  18 December 2023

BO YU Open the ORCID record for BO YU [Opens in a new window]  and
JIANKUI LI Open the ORCID record for JIANKUI LI [Opens in a new window]
BO YU*
Affiliation:
School of Mathematics, East China University of Science and Technology, Shanghai 200237, PR China
JIANKUI LI
Affiliation:
School of Mathematics, East China University of Science and Technology, Shanghai 200237, PR China e-mail: [email protected]
*
e-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Let H be a complex separable Hilbert space with 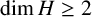$\dim H \geq 2$. Let 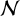$\mathcal {N}$ be a nest on H such that 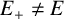$E_+ \neq E$ for any 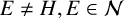$E \neq H, E \in \mathcal {N}$. We prove that every 2-local isometry of 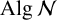$\operatorname {Alg}\mathcal {N}$ is a surjective linear isometry.

Keywords

nest algebraisometry2-local isometry

MSC classification

Primary: 47B49: Transformers, preservers (operators on spaces of operators)
Secondary: 47L35: Nest algebras, CSL algebras
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 110 , Issue 2 , October 2024 , pp. 367 - 376
Check for updates
Copyright
© The Author(s), 2023. Published by Cambridge University Press on behalf of Australian Mathematical Publishing Association Inc.

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

Footnotes

This research was partly supported by the National Natural Science Foundation of China (Grant No. 11871021.

References

Al-Halees, H. and Fleming, R., ‘On 2-local isometries on continuous vector-valued function spaces’, J. Math. Anal. Appl. 354(1) (2009), 70–77.10.1016/j.jmaa.2008.12.023CrossRefGoogle Scholar
Arazy, J. and Solel, B., ‘Isometries of nonselfadjoint operator algebras’, J. Funct. Anal. 90(2) (1990), 284–305.10.1016/0022-1236(90)90085-YCrossRefGoogle Scholar
Hou, J. and Cui, J., ‘Rank-1 preserving linear maps on nest algebras’, Linear Algebra Appl. 369 (2003), 263–277.10.1016/S0024-3795(02)00725-5CrossRefGoogle Scholar
Jiménez-Vargas, A., Li, L., Peralta, A. M., Wang, L. and Wang, Y.-S., ‘2-local standard isometries on vector-valued Lipschitz function spaces’, J. Math. Anal. Appl. 461(2) (2018), 1287–1298.10.1016/j.jmaa.2018.01.029CrossRefGoogle Scholar
Kowalski, S. and Słodkowski, Z., ‘A characterization of multiplicative linear functionals in Banach algebras’, Studia Math. 67(3) (1980), 215–223.10.4064/sm-67-3-215-223CrossRefGoogle Scholar
Li, L., Liu, S. and Ren, W., ‘2-local isometries on vector-valued differentiable functions’, Ann. Funct. Anal. 14(4) (2023), Article no. 70.10.1007/s43034-023-00295-9CrossRefGoogle Scholar
Longstaff, W. E., ‘Strongly reflexive lattices’, J. Lond. Math. Soc. (2) 11(4) (1975), 491–498.10.1112/jlms/s2-11.4.491CrossRefGoogle Scholar
Molnár, L., ‘2-local isometries of some operator algebras’, Proc. Edinb. Math. Soc. (2) 45(2) (2002), 349–352.10.1017/S0013091500000043CrossRefGoogle Scholar
Molnár, L., ‘On 2-local *-automorphisms and 2-local isometries of B(H)’, J. Math. Anal. Appl. 479(1) (2019), 569–580.10.1016/j.jmaa.2019.06.038CrossRefGoogle Scholar
Moore, R. L. and Trent, T. T., ‘Isometries of nest algebras’, J. Funct. Anal. 86(1) (1989), 180–209.10.1016/0022-1236(89)90069-4CrossRefGoogle Scholar
Moore, R. L. and Trent, T. T., ‘Isometries of certain reflexive operator algebras’, J. Funct. Anal. 98(2) (1991), 437–471.10.1016/0022-1236(91)90086-KCrossRefGoogle Scholar
Mori, M., ‘On 2-local nonlinear surjective isometries on normed spaces and ${C}^{\ast }$ -algebras’, Proc. Amer. Math. Soc. 148(6) (2020), 2477–2485.10.1090/proc/14949CrossRefGoogle Scholar
Šemrl, P., ‘Local automorphisms and derivations on $B(H)$ ’, Proc. Amer. Math. Soc. 125(9) (1997), 2677–2680.10.1090/S0002-9939-97-04073-2CrossRefGoogle Scholar