Hostname: page-component-669899f699-7tmb6 Total loading time: 0 Render date: 2025-04-28T14:36:23.068Z Has data issue: false hasContentIssue false
  • English
  • Français

A multi-layer Kriging surrogate model for the reliability analysis of variable stator vanes in aero engines

Published online by Cambridge University Press:  16 December 2024

J. Fan Open the ORCID record for J. Fan [Opens in a new window] ,
H. Xu Open the ORCID record for H. Xu [Opens in a new window] ,
Q. Meng  and
S. Xu
J. Fan*
Affiliation:
School of Energy and Power Engineering, Beihang University, Beijing, China Beijing Key Laboratory of Aero-Engine Structure and Strength, Beijing, China Collaborative Innovation Center of Advanced Aero-Engine, Beijing, China
H. Xu
Affiliation:
School of Energy and Power Engineering, Beihang University, Beijing, China
Q. Meng
Affiliation:
School of Energy and Power Engineering, Beihang University, Beijing, China
S. Xu
Affiliation:
Institute of Mechanics, Chinese Academy of Sciences, Beijing, China
*
Corresponding author: J. Fan; Email: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

The variable stator vanes (VSV) are a set of typical spatial linkage mechanisms widely used in the variable cycle engine compressor. Various factors influence the angle adjustment precision of the VSV, leading to the failure of the mechanism. The reliability analysis of VSV is a complex task due to the involvement of multiple components, high dimensionality input and computational inefficiency. Considering the hierarchical characteristics of VSV structure, we propose a novel multi-layer Kriging surrogate (MLKG) for the reliability analysis of VSV. The MLKG combines multiple Kriging surrogate models arranged in a hierarchical structure. By breaking the problem down into more minor problems, MLKG works by presenting each small problem as a Kriging model and reducing the input dimension of the sub-layer Kriging model. In this way, the MLKG can capture the complex interactions between the inputs and outputs of the problem while maintaining a high degree of accuracy and efficiency. This study proves the error propagation process of MLKG. To evaluate MLKG’s accuracy, we test it on two typical high-dimensional non-linearity functions (Rosenbrock and Michalewicz function). We compared MLKG with some contemporary KG surrogate modeling techniques using mean squared error (MSE) and R square (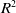${R^2}$). Results show that MLKG achieves an excellent level of accuracy for reliability analysis in high-dimensional problems with a small number of sample points.

Keywords

surrogate modelreliability analysisvane stator variablesaero-engine
Type
Research Article
Information
The Aeronautical Journal , Volume 129 , Issue 1331 , January 2025 , pp. 123 - 143
Check for updates
Copyright
© The Author(s), 2024. Published by Cambridge University Press on behalf of Royal Aeronautical Society

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Zhang, B., Liu, S. and Liu, H. Research on influence of geometric adjustment on performance of variable cycle engine, 2018 2nd International Conference on Aerospace Technology, Communications And Energy Systems (ATCES 2018), vol. 449, IoP Publishing Ltd, 2018, Bristol, p 012022. https://doi.org/10.1088/1757-899X/449/1/012022 CrossRefGoogle Scholar
Wang, Z., Li, J., Fan, K. and Li, S. The off-design performance simulation of marine gas turbine based on optimum scheduling of variable stator vanes, Math. Probl. Eng. 2017, 2017, 2671251. https://doi.org/10.1155/2017/2671251 CrossRefGoogle Scholar
Michael, H. Simulation and optimization of an adjustable inlet guide vane for industrial turbo compressors, Berlin, 2008.Google Scholar
Peng, D.C. Numerical predictions of rotating stall in an axial multi-stage compressor, Vancouver, 2011.CrossRefGoogle Scholar
Zhang, S. Research on Analysis Methods for the Motion Characteristics of Static Blade Adjustment Mechanisms, Nanjing University of Aeronautics and Astronautics, 2015.Google Scholar
Xie, J., Jia, Z. and Yuan, S. Research status of adjustable mechanism of variable cycle engine, Aero Engine Control, 2019, 1.Google Scholar
Zhang, H., Song, L.K., Bai, G.C., et al. Active extremum Kriging-Based multi-level linkage reliability analysis and its application in aeroengine mechanism systems, Aerospace Science and Technology, 2022, 131, p 107968.CrossRefGoogle Scholar
Zhu, S.-P., Huang, H.-Z., Smith, R., Ontiveros, V., He, L.-P. and Modarres, M. Bayesian framework for probabilistic low cycle fatigue life prediction and uncertainty modeling of aircraft turbine disk alloys, Probab. Eng. Mech., 2013, 34, pp 114–122.CrossRefGoogle Scholar
Xiao, N.-C., Zuo, M.J., and Zhou, C. A new adaptive sequential sampling method to construct surrogate models for efficient reliability analysis, Reliab. Eng. Syst. Safety, 2018, 169, pp 330–338.CrossRefGoogle Scholar
Huang, B. and Du, X. Probabilistic uncertainty analysis by mean-value first order Saddlepoint Approximation, Reliab. Eng. Syst. Safety, 2008, 93, pp 325–336.CrossRefGoogle Scholar
Gao, Z., Chen, Y. and Yi, Z. A Novel method to compute the weights of neural networks, Neurocomputing, 2020, 407, pp 409–427.CrossRefGoogle Scholar
Heydt, G.T. and Graf, T.J. Distribution system reliability evaluation using enhanced samples in a Monte Carlo approach, IEEE Trans. Power Syst. 2010, 25, pp 2006–2008. https://doi.org/10.1109/TPWRS.2010.2045929 CrossRefGoogle Scholar
Li, F.X., Brown, R.E. and Freeman, L.A.A. A linear contribution factor model of distribution reliability indices and its applications in Monte Carlo simulation and sensitivity analysis, IEEE Trans. Power Syst., 2003, 18, pp 1213–1215.Google Scholar
Bhosekar, A. and Ierapetritou, M. Advances in surrogate based modeling, feasibility analysis, and optimization: A review, Comput. Chem. Eng., 2018, 108, pp 250–267.CrossRefGoogle Scholar
Li, M., Wang, R.-Q. and Jia, G. Efficient dimension reduction and surrogate-based sensitivity analysis for expensive models with high-dimensional outputs, Reliab. Eng. Syst. Safety, 2020, 195, p 106725.CrossRefGoogle Scholar
Li, Y. and Shi, J. An improved high-dimensional kriging surrogate modeling method through principal component dimension reduction, Mathematics, 2021, 9, p 1985.CrossRefGoogle Scholar
Han, S., Song, W., Han, Z. and Wang, L. Aerodynamic inverse design method based on gradient-enhanced Kriging model, Acta Aeronautica et Astronautica Sinica, 2017, 38, pp 138–152.Google Scholar
Hu, J., Rui, S., Gao, R., Gou, J. and Gong, C. Hybrid optimization method for structural layout and size of flight vehicles, Acta Aeronaut. Astronaut. Sinica, 2022, 43, pp 368–378.Google Scholar
Zhou, Y. and Lu, Z. An enhanced Kriging surrogate modeling technique for high-dimensional problems, Mech. Syst. Signal Process., 2020, 140, p 106687.CrossRefGoogle Scholar
Deng, J. Structural reliability analysis for implicit performance function using radial basis function network, Int. J. Solids Struct., 2006, 43, pp 3255–3291.CrossRefGoogle Scholar
Lataniotis, C., Marelli, S. and Sudret, B. Extending classical surrogate modeling to high dimensions through supervised dimensionality reduction: A data-driven approach, Int. J. Uncertainty Quantif., 2020, 10, pp 55–82.CrossRefGoogle Scholar
Guo, Y., Mahadevan, S., Matsumoto, S., et al. Investigation of surrogate modeling options with high-dimensional input and output, AIAA Journal, 2023, 61, (3), pp 1334–1348.CrossRefGoogle Scholar
Bouhlel, M.A. and Bartoli, N. Improving kriging surrogates of high-dimensional design models by Partial Least Squares dimension reduction, Struct. Multidiscip. Optim., 2016, 53, pp 935–952.CrossRefGoogle Scholar
Chen, G., Zhang, K., Xue, X., Zhang, L., Yao, J., Sun, H., et al. Surrogate-assisted evolutionary algorithm with dimensionality reduction method for water flooding production optimization, J. Pet. Sci. Eng., 2020, 185, p 106633.CrossRefGoogle Scholar
Dai, P., Ding, X. and Wang, Q. Dimension reduction based linear surrogate variable approach for model free variable selection, J. Stat. Plann. Inference, 2016, 169, pp 13–26.CrossRefGoogle Scholar
Cheng, K., Lu, Z., Zhou, Y., Shi, Y. and Wei, Y. Global sensitivity analysis using support vector regression, Appl. Math. Model., 2017, 49, pp 587–598.CrossRefGoogle Scholar
Borgonovo, E., Apostolakis, G.E., Tarantola, S. and Saltelli, A. Comparison of global sensitivity analysis techniques and importance measures in PSA, Reliab. Eng. Syst. Safety, 2003, 79, pp 175–185.CrossRefGoogle Scholar
Tripathy, R.K. and Bilionis, I. Deep UQ: Learning deep neural network surrogate models for high dimensional uncertainty quantification, J. Comput. Phys., 2018, 375, pp 565–588.CrossRefGoogle Scholar
Zhao, L., Wang, P., Song, B., Wang, X. and Dong, H. An efficient kriging modeling method for high-dimensional design problems based on maximal information coefficient, Struct. Multidiscip. Optim., 2020, 61, pp 39–57.CrossRefGoogle Scholar
Morris, M.D. Factorial sampling plans for preliminary computational experiments, Technometrics, n.d., 33, (2). Taylor & Francis Online.Google Scholar