Hostname: page-component-669899f699-7xsfk Total loading time: 0 Render date: 2025-04-28T12:08:37.987Z Has data issue: false hasContentIssue false
  • English
  • Français

Interlacement limit of a stopped random walk trace on a torus

Part of: Special processes

Published online by Cambridge University Press:  24 August 2023

Antal A. Járai  and
Minwei Sun Open the ORCID record for Minwei Sun [Opens in a new window]
Antal A. Járai*
Affiliation:
University of Bath
Minwei Sun*
Affiliation:
University of Bath
*
*Postal address: Department of Mathematical Sciences, University of Bath, Claverton Down, Bath BA2 7AY, UK.
*Postal address: Department of Mathematical Sciences, University of Bath, Claverton Down, Bath BA2 7AY, UK.
Get access Rights & Permissions [Opens in a new window]

Abstract

We consider a simple random walk on 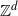$\mathbb{Z}^d$ started at the origin and stopped on its first exit time from 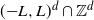$({-}L,L)^d \cap \mathbb{Z}^d$. Write L in the form 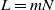$L = m N$ with 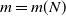$m = m(N)$ and N an integer going to infinity in such a way that 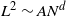$L^2 \sim A N^d$ for some real constant 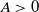$A \gt 0$. Our main result is that for 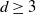$d \ge 3$, the projection of the stopped trajectory to the N-torus locally converges, away from the origin, to an interlacement process at level 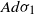$A d \sigma_1$, where 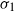$\sigma_1$ is the exit time of a Brownian motion from the unit cube 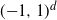$({-}1,1)^d$ that is independent of the interlacement process. The above problem is a variation on results of Windisch (2008) and Sznitman (2009).

Keywords

Interlacementhitting probabilityhashingloop-erased random walk

MSC classification

Primary: 60K35: Interacting random processes; statistical mechanics type models; percolation theory
Type
Original Article
Information
Advances in Applied Probability , Volume 56 , Issue 1 , March 2024 , pp. 354 - 388
Check for updates
Copyright
© The Author(s), 2023. Published by Cambridge University Press on behalf of Applied Probability Trust

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Černý, J. and Teixeira, A. (2016). Random walks on torus and random interlacements: Macroscopic coupling and phase transition. Ann. Appl. Prob. 26, 2883–2914.CrossRefGoogle Scholar
Dhar, D. (2006). Theoretical studies of self-organized criticality. Physica A 369, 29–70.CrossRefGoogle Scholar
Drewitz, A., Ráth, B. and Sapozhnikov, A. (2014). An Introduction to Random Interlacements, 1st edn. Springer, Berlin.CrossRefGoogle Scholar
Durrett, R. (2019). Probability: Theory and Examples, 5th edn. Cambridge University Press.CrossRefGoogle Scholar
Hebisch, W. and Saloff-Coste, L. (1993). Gaussian estimates for Markov chains and random walks on groups. Ann. Prob. 21, 673–709.CrossRefGoogle Scholar
Járai, A. A. (2018). Sandpile models. Prob. Surveys 15, 243–306.CrossRefGoogle Scholar
Járai, A. A. and Sun, M. (2019). Toppling and height probabilities in sandpiles. J. Statist. Mech. 2019, article no. 113204.CrossRefGoogle Scholar
Lawler, G. F. (2013). Intersections of Random Walks. Birkhäuser, New York.CrossRefGoogle Scholar
Lawler, G. F. and Limic, V. (2010). Random Walk: A Modern Introduction. Cambridge University Press.CrossRefGoogle Scholar
Levin, D. A., Peres, Y. and Wilmer, E. L. (2017). Markov Chains and Mixing Times, 2nd edn. American Mathematical Society, Providence, RI.CrossRefGoogle Scholar
Redig, F. (2006). Mathematical aspects of the abelian sandpile model. In Mathematical Statistical Physics: Lecture Notes of the Les Houches Summer School 2005, eds Bovier, A., Dunlop, F., Van Enter, A., F. den Hollander and J. Dalibard, Elsevier, Amsterdam, pp. 657–729.CrossRefGoogle Scholar
Sznitman, A.-S. (2009). Random walks on discrete cylinders and random interlacements. Prob. Theory Relat. Fields 145, 143–175.CrossRefGoogle Scholar
Sznitman, A.-S. (2010). Vacant set of random interlacements and percolation. Ann. Math. 171, 2039–2087.CrossRefGoogle Scholar
Sznitman, A.-S. (2012). Topics in Occupation Times and Gaussian Free Fields. European Mathematical Society, Zürich.CrossRefGoogle Scholar
Windisch, D. (2008). Random walk on a discrete torus and random interlacements. Electron. Commun. Prob. 13, 140–150.CrossRefGoogle Scholar